Proximal Policy Optimization (PPO, PPO-Clip, PPO-Penalty) 是由TRPO的作者Schulman等人于2017年提出的策略梯度类算法。PPO算法的思路和TRPO一致,都是想在优化时采取尽可能大的步幅但又不能太大以至于产生崩坏。相比于比TRPO,PPO实现起来更简单,泛化能力更强,可以使用随机梯度下降(SGD)进行优化。
背景
PPO的背景与TRPO的背景一致,最终TRPO推导出如下的带约束优化问题: \[ \max_{\theta}\mathbb{E}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}A_t]\\ \text{subject to }\mathbb{E}_t[\text{KL}[\pi_{\theta_{old}}(\cdot|s_t), \pi_\theta(\cdot|s_t)]] \] 令 \(r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\) 为新旧策略的概率比(易知 \(r_t(\theta_{old}) = 1\))。TRPO最大化的替代目标(surrogate objective)可以写为如下形式: \[ L^{CPI}(\theta)=\mathbb{E}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}A_t]=\mathbb{E}_t[r_t(\theta)A_t] \] 如果不加约束的话,直接优化该目标会产生巨大的更新,导致更新不稳定甚至崩溃。所以需要考虑一种惩罚方法,使 \(r_t(\theta)\) 接近 \(1\)。
PPO-Clip
PPO-Clip的目标函数为: \[ L^{CLIP}(\theta)=\mathbb{E}_t[\min(r_t(\theta)A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)A_t)] \] 其中 \(\epsilon\) 为超参数控制截断率,取值通常比较小(0.2左右)。
上述目标函数的第一项与 \(L^{CPI}\) 一致,第二项则是为了限制更新幅度(施加惩罚),控制 \(r_t(\theta) \in [1-\epsilon, 1+\epsilon]\)。可见 \(L^{CLIP}(\theta)\) 是 \(L^{CPI}(\theta)\) 的一个下界。
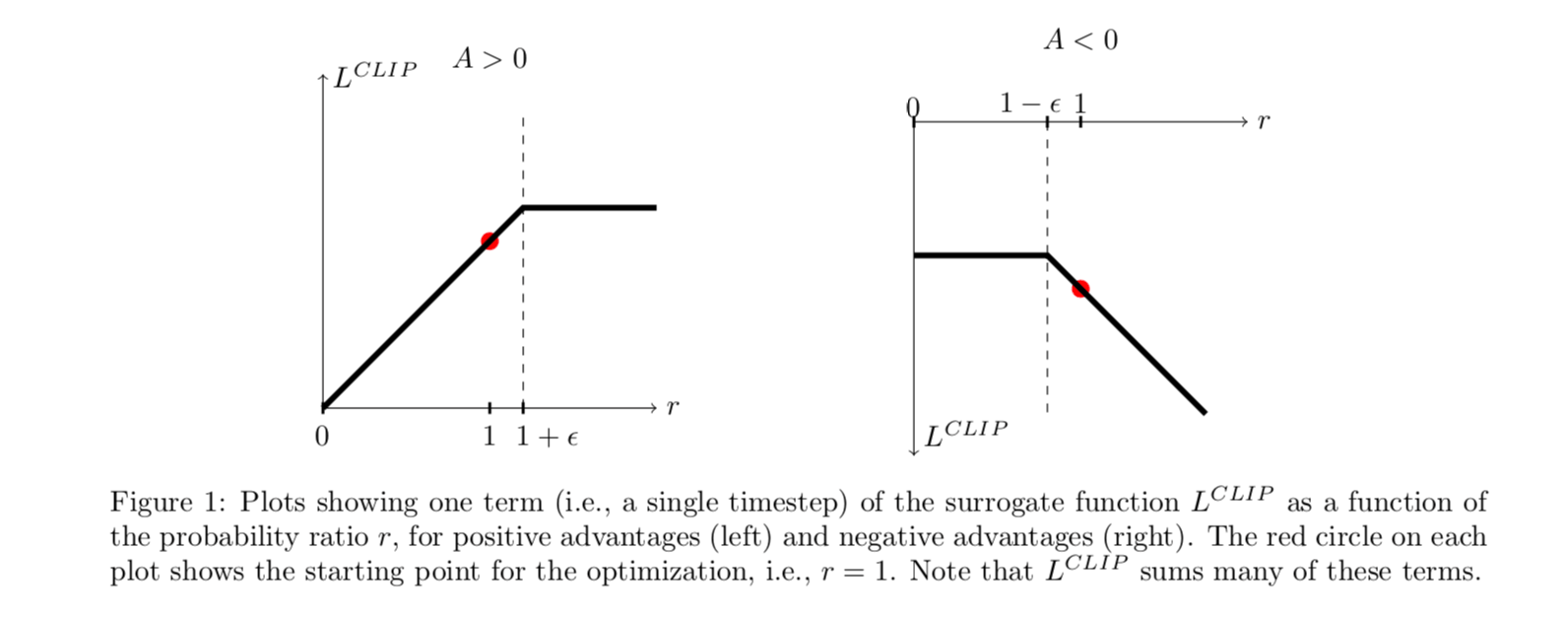
上图显示了 \(\text{clip}\) 函数的工作方式:
- 当 \(A > 0\) 时,如果想使目标函数取得更大的值,就需要增大 \(\pi_\theta(a_t|s_t)\) 的值,也就是增大 \(r_t(\theta)\) 。但是式中的 \(\min\) 函数限制了 \(r_t(\theta)\) 最大取到 \(1+\epsilon\),所以新策略再远离旧策略(\(r_t(\theta)\) 继续增大)并不会带来更多地好处。
- 当 \(A < 0\) 时,如果想使目标函数取得更大的值,就需要减小 \(\pi_\theta(a_t|s_t)\) 的值,也就是减小 \(r_t(\theta)\) 。但是式中的 \(\min\) 函数限制了 \(r_t(\theta)\) 最小取到 \(1-\epsilon\),所以新策略再远离旧策略(\(r_t(\theta)\) 继续减小)并不会带来更多地好处。
在实现中,目标函数通常使用更简单的形式: \[ L^{CLIP}(s, a, \theta_k, \theta)=\min(\frac{\pi_\theta(a|s)}{\pi_{\theta_{k}}(a|s)}A^{\pi_{\theta_k}}(s, a), g(\epsilon, A^{\pi_{\theta_k}}(s, a))) \] 其中, \[ g(\epsilon, A^{\pi_{\theta_k}}(s, a))=\begin{cases} (1+\epsilon)A, & \mbox{if }A ≥0 \\ (1-\epsilon)A, & \mbox{if }A<0 \end{cases} \]
注:即便对 \(r_t(\theta)\) 加上截断,新策略仍染有可能偏离旧策略很远,不过有很多trick来处理这个问题。其中一个特别简单的处理方式就是:如果新策略和旧策略的平均KL距离大于某个阈值,则停止进行更新(early stopping)。
相比于TRPO,由于没有了KL约束,PPO可以用SGD来进行优化,实现简单很多。
PPO-Clip算法
PPO-Penalty
这种方法使用KL距离作为惩罚项,关键在于求出能够自适应多种任务的惩罚因子 \(\beta\)。算法的逻辑为,在每次策略进行更新时:
使用SGD优化目标函数: \[ L^{KLPEN}(\theta)=\mathbb{E}_t\left[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}A_t-\beta\cdot\text{KL}[\pi_{old}(a_t|s_t), \pi_\theta(a_t|s_t)]\right] \]
计算 \(d = \mathbb{E}\left[\text{KL}[\pi_{\theta_{old}}(\cdot|s_t), \pi_\theta(\cdot|s_t)]\right]\)
- 如果 \(d < d_{targ}/1.5\),则 \(\beta \leftarrow \beta/2\)
- 如果 \(d > d_{targ} \times 1.5\),则 \(\beta \leftarrow\beta \times 2\)
其中,\(d_{targ}\) 为超参数。
注:PPO-Penalty 没有 PPO-Clip 效果好。
实验和总结
特点
- 训练稳定
- 通过限制 \(r_t(\theta)\) 来找到尽可能大的并且合理的步长
- on-policy 算法
- 可用于离散和连续的动作空间
- 相比于TRPO,PPO实现简单,效果更好
实验性能
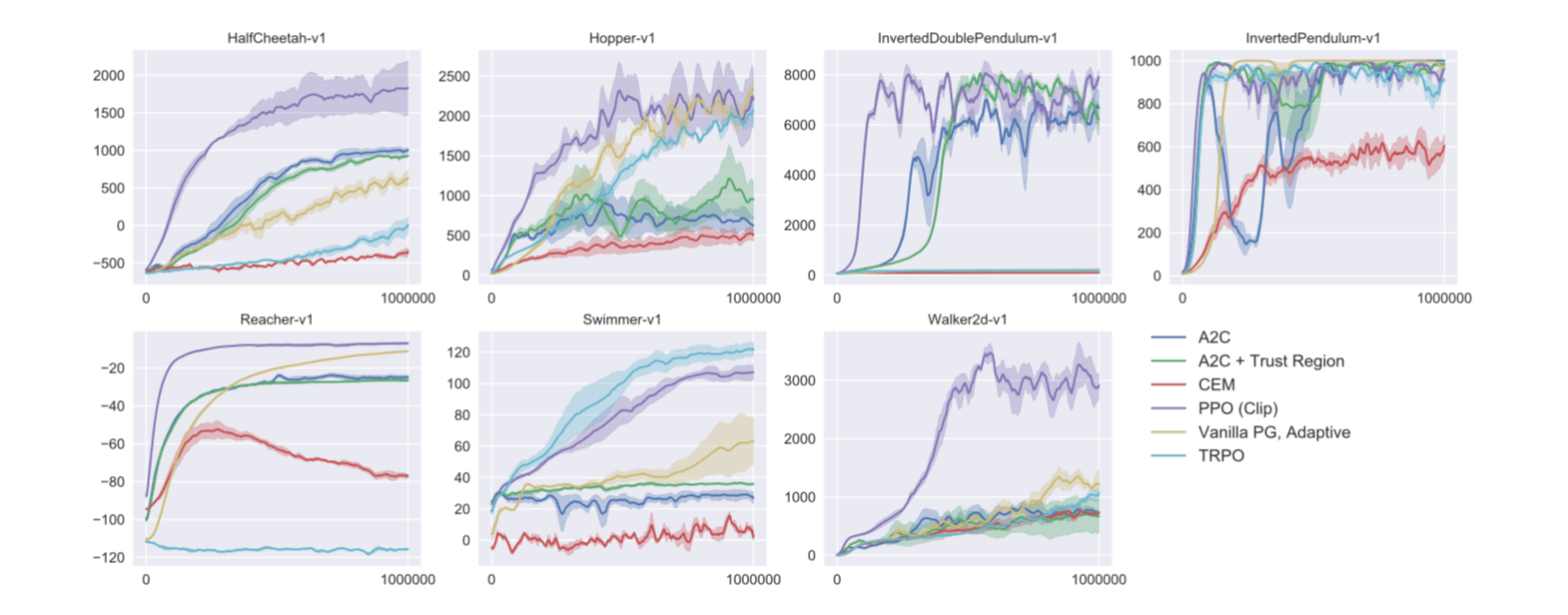
在大部分 MuJoCo 环境中强于其他策略梯度类算法,在Atari环境中,表现仅次于ACER,但是学习速度优于ACER。

代码
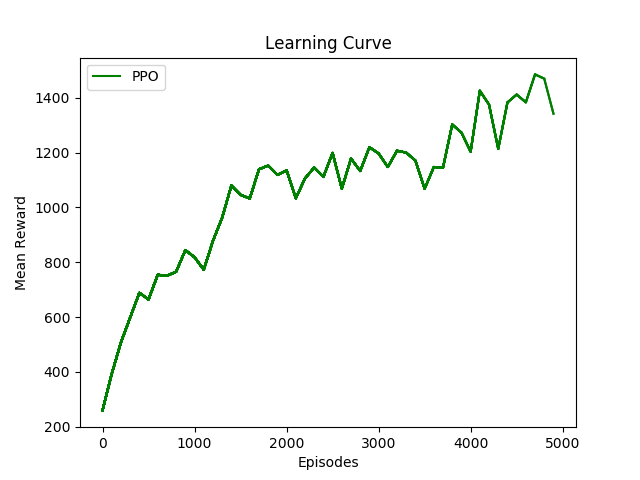
自己也实现了一下PPO-Clip算法,代码在这里。下图显示了在 OpenAI Gym 上的 MsPacman-ram-v0 环境上的测试结果:
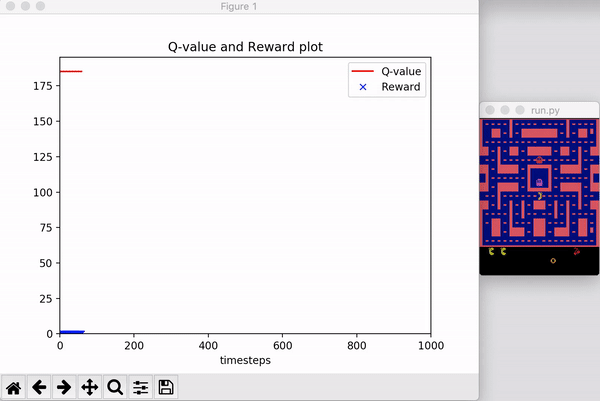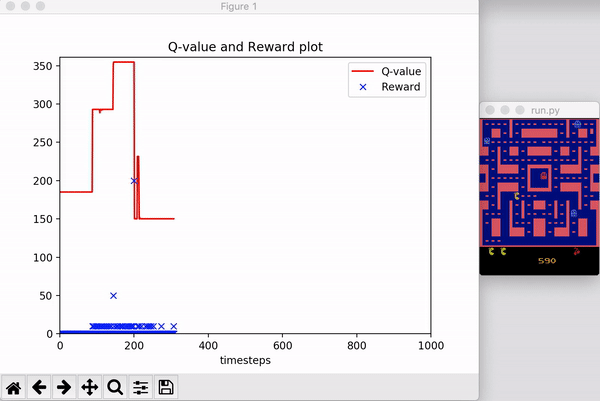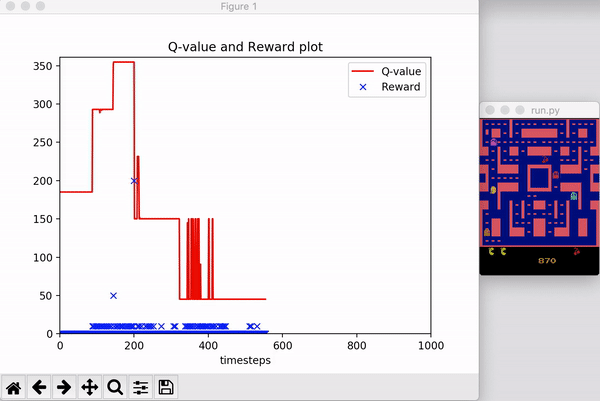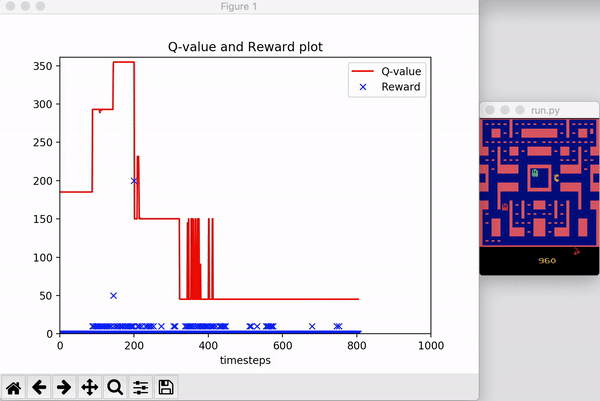

References
[1] https://arxiv.org/abs/1707.06347
[2] https://spinningup.openai.com/en/latest/algorithms/ppo.html
